Kanatçıklı Borulu Isı Değiştirgeçlerinde Boru İz takibi ile Evaporatör ve Kondenser Hesaplamaları
Özet
Kanatçıklı borulu ısı değiştirgeçleri günümüzde endüstriyel ve ev tipi klimalarda yaygın olarak kullanılmaktadır. Ev tipi klimalar, VRF-VRV sistemleri, çatı tipi klima cihazları, havuz nem alma cihazları ve klima santrallerindeki direkt genleşmeli sistemler bu tip ısı değiştirgeçlerinin kullanıldığı alanlara en yaygın örneklerdir. Klima sistemlerinde genel olarak; iç hava şartlandırma tarafında kanatçıklı-borulu ısı değiştirgeçleri kullanılırken, yoğuşturucu olarak kanatçıklı-borulu ya da mikro kanallı eşanjörler kullanılmaktadır. Bu çalışmada kanatçıklı borulu buharlaştırıcı ve yoğuşturucu hesaplamalarının matematiksel modeli incelenmiştir. Ayrıca, kesit-kesit metoduna göre, homojen ve homojen olmayan hava dağılımının, buharlaştırıcı ile yoğuşturucu devrelerindeki akışkan debilerine etkisi ve performans bilgileri irdelenmiştir.
Anahtar kelimeler: Kanatçıklı borulu ısı değiştirgeci, evaporatör, kondenser, HAD analizi, hava dağılımı, devreleme algoritması
Giriş
Kanatçıklı borulu ısı değiştirgeçleri günümüzde endüstriyel ve ev tipi klimalarda yaygın olarak kullanılmaktadır. Ev tipi klimalar, VRF-VRV sistemleri, çatı tipi klima cihazları, havuz nem alma cihazları ve klima santrallerindeki direkt genleşmeli sistemler bu tip ısı değiştirgeçlerinin kullanıldığı alanlara en yaygın örneklerdir. Klima sistemlerinde genel olarak; iç hava şartlandırma tarafında kanatçıklı-borulu ısı değiştirgeçleri kullanılırken, yoğuşturucu olarak kanatçıklı-borulu ya da mikro kanallı eşanjörler kullanılmaktadır. Bu çalışmada kanatçıklı borulu buharlaştırıcı ve yoğuşturucu hesaplamalarının matematiksel modeli incelenmiştir. Ayrıca, kesit-kesit metoduna göre, homojen ve homojen olmayan hava dağılımının, buharlaştırıcı ile yoğuşturucu devrelerindeki akışkan debilerine etkisi ve performans bilgileri irdelenmiştir.
Matematiksel model
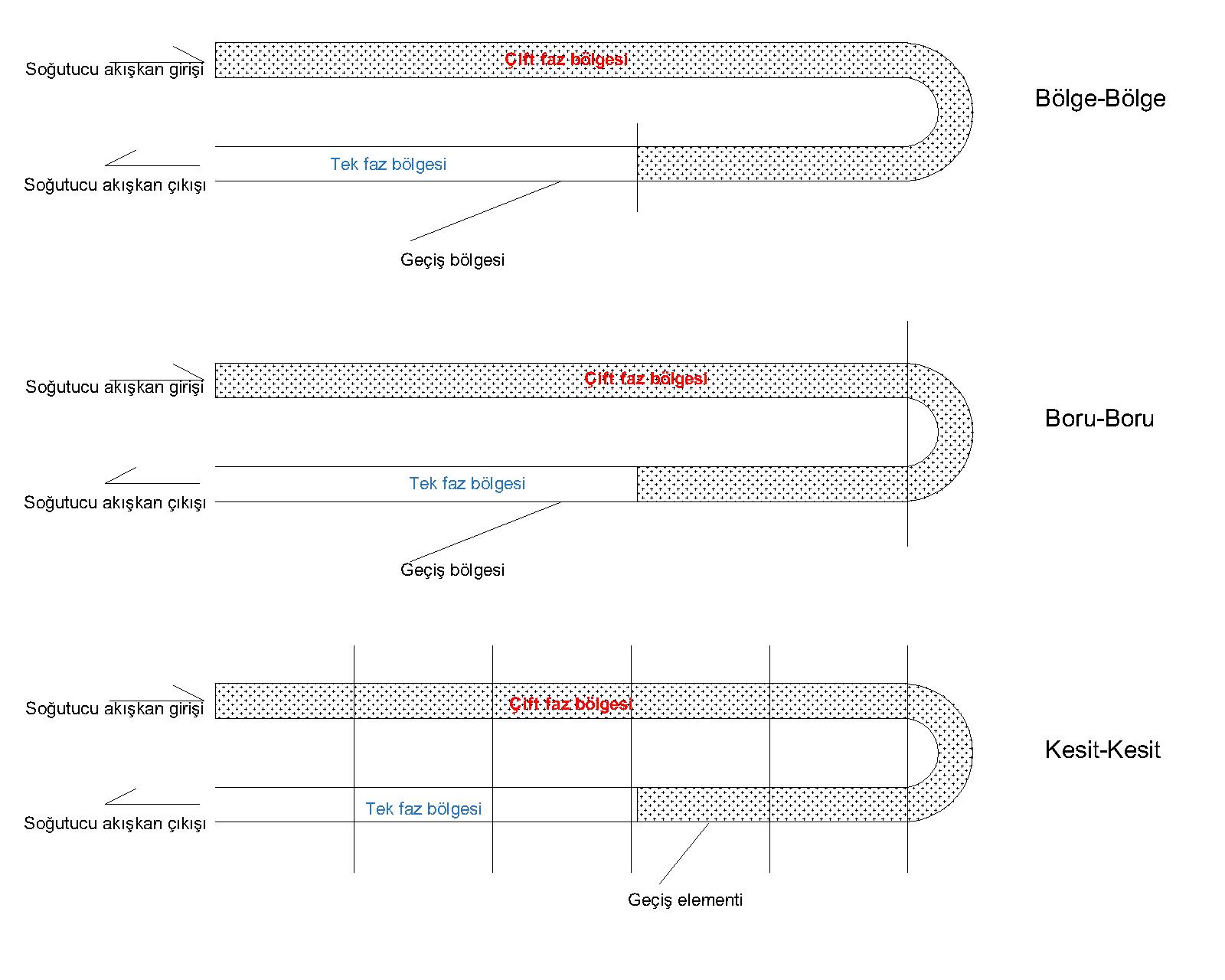
Kanatçıklı borulu ısı değiştirgeci hesaplarında, literatürde 3 tip matematiksel model kullanılmaktadır; Bölge-bölge (Zone by zone), boru-boru (tube by tube), kesit-kesit (segment by segment). Bölge-bölge hesabında, eşdeğer boru dizilimi ve eşit dağılımlı hava akımı tüm ısı değiştirgeci sistemine uygulanırken, boru-boru ve kesit-kesit metodunda ısı değiştirgecinin boru dizilimine göre ısı geçişi, basınç kaybı ve kapasite hesapları yapılmaktadır. Dolayısıyla boru-boru ve kesit-kesit metotlarında her akışkan devresindeki basınç kaybı, kütlesel debi ve faz değişim sıcaklıkları ayrı ayrı hesaplanabilmektedir. Literatürde Fisher ve ark. (Fischer, ve diğerleri, 1988), ile Mullen ve Ark. (Mullen, ve diğerleri, 1997), bölge- bölge metodunu kullanırken, boru-boru metodunu Domanski ve arkadaşları (Domanski, ve diğerleri, 1983) ile Liang ve arkadaşları (Liang, ve diğerleri, 1998) kullanmış, kesit- kesit metodunu ise Jiang (Jiang, ve diğerleri, 2006) ve arkadaşları ile Ragazzi (Ragazzi, ve diğerleri, 1991) gibi araştımacılar tercih etmiştir. Şekil 2.1’de 3 modelin şematik görseli yer almaktadır. Bu çalışmada boru yerleşimini yapmak, farklı hava akış profillerini kullanabilmek ve akışkan basınç kayıplarının faz değişim sıcaklığına etkisini de inceleyebilmek için kesit-kesit modeli kullanılmıştır.
1.1 Isı transferi hesaplamaları
Isı transferi hesaplamalarında iki metot kullanılmaktadır; Ԑ-NTU ve LMTD (Incorpera, ve diğerleri, 2006). LMTD metodunda akışkan çıkış sıcaklığı hesaba iteratif giriş parametresi olarak girilirken, Ԑ-NTU metodunda çıkış sıcaklığı girilmesine gerek yoktur. Dolayısıyla Ԑ-NTU metodu hesaplama zaman performansı için daha uygun bir metottur. Bu çalışmada ısı transfer hesabında Ԑ-NTU metodu, kanatçık veriminde ise Schmidt metodu (Schmidt, 1949) kullanılmıştır. Kuru yüzeyler için aşağıdaki formüller kullanılırken ıslak yüzeyler için Harms ve arkadaşlarının (Harms, ve diğerleri, 2003) oluşturduğu modifiye edilmiş formüller kullanılmıştır.
Akışkan tarafı ısı transfer katsayısı ve basınç kaybı
Literatürde, yoğuşma ve buharlaşma safhaları için geliştirilmiş birçok ampirik formül bulunmaktadır. Bu çalışmada, validasyon aralığı geniş ve akışkan kütlesel debisine göre akış profillerinin en detaylı incelendiği Thome ve arkadaşlarının geliştirdiği yoğuşma (Thome, ve diğerleri, 2003) ve buharlaşma (Thome, ve diğerleri, 2005) formülleri kullanılmıştır. Tek faz da ise Gnelski’nin geliştirdiği formüller kullanılmıştır. (Gnielinski, 1976)
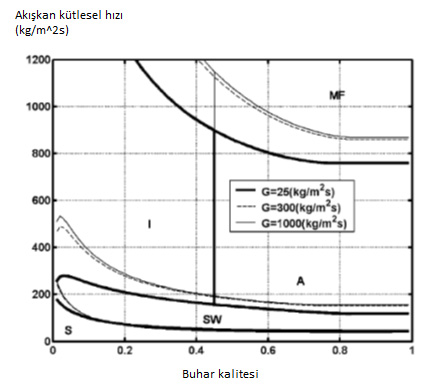
Şekil 2. 40° C’de R134 a gazı boru iç çapı:8 mm’de buhar oranı ve akışkan kütlesel hızına göre akış profilleri (Thome, ve diğerleri, 2003)
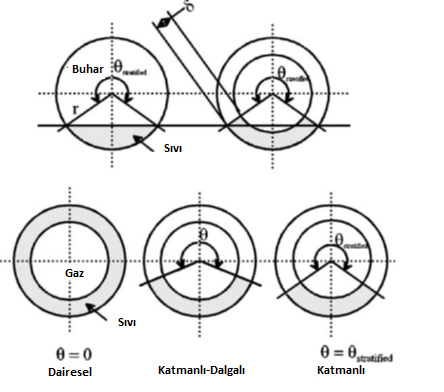
Şekil 3. Yoğuşma akış tipine göre kuruluk açıları tanımı (Thome, ve diğerleri, 2003)
Akışkan basınç kaybı üç ana kola ayrılmaktadır; Sürtünme, yer çekimi ve hızlanma kaynaklı. En baskın olan ise sürtünmeye dayalı olan elamandır. Sürtünmeye dayalı basınç kaybında buharlaşma durumunda yine Thome ve arkadaşlarının (Thome, ve diğerleri, 2007) geliştirmiş olduğu formüller kullanılırken, yoğuşmada Souza ve arkadaşlarının (Souza, ve diğerleri, 1992) geliştirmiş olduğu formüller kullanılmıştır. Tek fazlı durumda da Ragazzi ve arkadaşlarının geliştirmiş olduğu formüller kullanılmıştır.
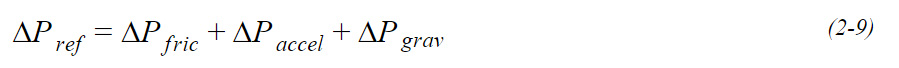
Hava tarafı ısı transfer katsayısı ve basınç kaybı
Kanatçıklı borulu ısı değiştirgeçlerinde düz, dalgalı, louver ve slit kanatçık olarak dört farklı kanatçık tipi kullanılmaktadır. Kanatçık yapıları değiştikçe ısı transferi ve basınç kaybı katsayıları değişmektedir. Bu çalışmada dalgalı kanatçık yapısı baz alınmış ve bunun için Wang ve arkadaşlarının (Wang, ve diğerleri, 2002) Colburn J ve fan sürtünme faktörüne göre geliştirmiş olduğu formüller kullanılmıştır. Katsayılar her kesit için farklı hava giriş çıkış koşullarında, tüm eşanjör yüzeyi için hesaplanmıştır.
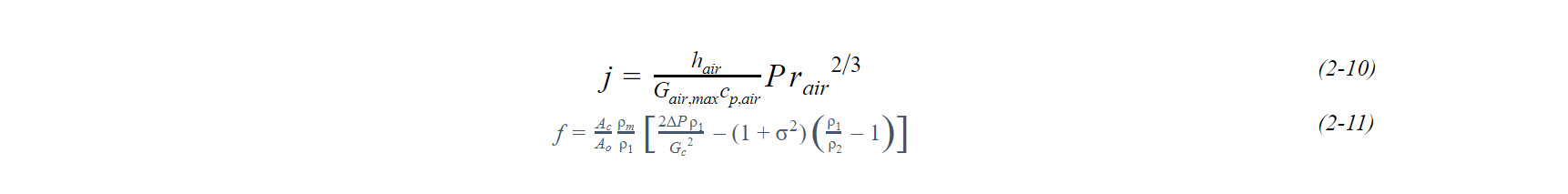
Wang ve arkadaşlarının oluşturduğu formüller aşağıdaki gibi geçerlilik alanına sahiptir.
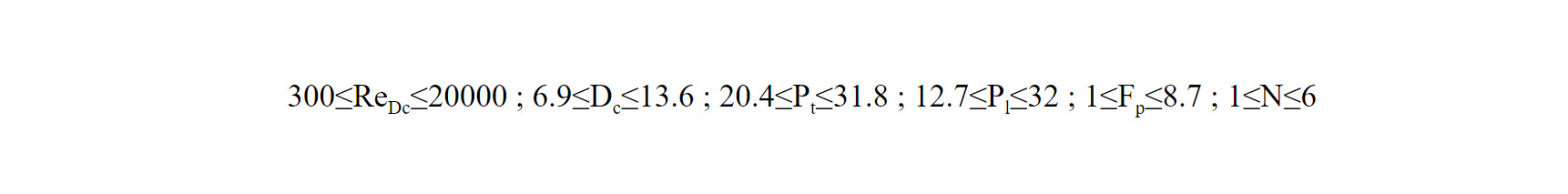
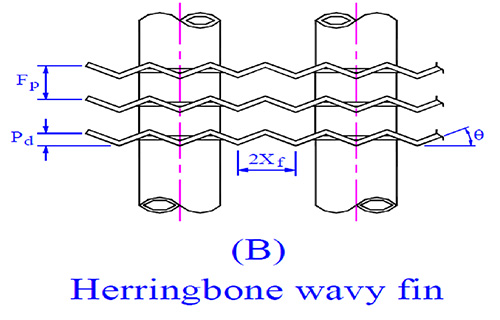
Şekil 4. Dalgalı kanatçıklı geometrik parametreler (Wang, 2000)
Boru dizilimi
Kanatçıklı borulu sistemlerin kapasite hesaplamalarında boru iz takibi büyük önem taşımaktadır. Literatürde, Domanski ve Jiang gibi araştırmacıların boru iz takibi yapmak için geliştirdiği ve “Junction Tube Matrix” olarak adlandırdığı matriks sistemler bulunmaktadır (Jiang, ve diğerleri, 2006) (Domanski, P. A.; Yashar, D., 2004). Şekil 5’de elektrik devre analizine benzer yapıda incelenmiş bir devreleme sisteminin örneği verilmiştir. Şekil 5’te akışkanın yönleri sayfa içine ve dışına göre tarif edilmiş olup, çizgilerlerle de borulardan geçiş noktaları (kuruve yerleri) belirtilmiştir. Akışkan 1 ve 5. borulardan geçiş yapıp, 2 ve 6. boruları takip ederek 3 boruda birleşmiş, 7,4 ve 8 nolu boruları takip ederek akışkan devreden çıkmıştır. Bu örnekten yola çıkılarak, bu çalışmada da devredeki akışkan borulara giriş sıralaması ve yönleri tarif edilmiş ve iz takibi yapılmıştır. Boru iz takibi ile;
- Akışkan faz durumu ve basınç kayıpları her devre için hesaplanabilir.
- Akışkan debisi her devre için ayrı ayrı hesaplanabilir.
- Farklı devrelerde, farklı akışkan tipleri ile kapasite hesaplanabilir.
- Borular üzerinden geçen havanın homojen olmadığı durumlarda hesaplamalar yapılabilir.
Bu çalışmada da her boru üzerinden geçen hava miktarı HAD analizine göre yorumlanıp, homojen olmadığı duruma göre hava debisi değişkenliği sağlanmıştır. Her devrenin her borusundaki segmentlerde, akışkanın fiziksel durumuna bağlı olarak ısı transfer ve basınç kaybı hesapları yapılarak simülasyon tamamlanmıştır.
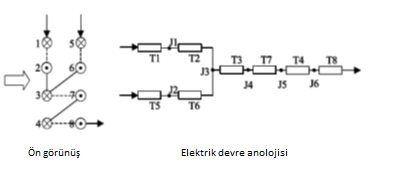
Şekil 5. Ayrışma ve birleşme boru dizilimi elektrik analojisi (Jiang, ve diğerleri, 2006)
Santral Kesitinde Isı Değiştirgeci Üzerinden Geçen Hava Akışının HAD Analizi
Bu çalışmada 1200×925 mm iç kesite sahip bir santralin hava dağılımı FDS (Versiyon 6.5.2) programında incelenmiştir. Hava debisi 8325 m3/h olan bir fan ile emiş hattındaki bir ısı değiştirgeci 3 boyutlu olarak simüle edilmiştir. Yandan tam merkezde alınan kesitte, ısı değiştirgecinin üst ve alt bölgelerinde hava hızının 0,25-1 m/s, orta taraflarında ise 2,5-3 m/s olduğu gözlemlenmiştir. Simülasyondaki matematiksel parametreler Tablo 1’de, simülasyon modellemesi Şekil 6’da, simülasyon çıktısı ise Şekil 7’de belirtilmiştir. Havanın fiziksel özellikleri 1 atm basınç, 20°C sıcaklıkta alınmış ve yoğunluğu 1,2kg/m3 olarak kabul edilmiştir. HAD analizinde mesh sayısından bağımsızlaştırma yapılmamıştır.
Tablo 1. HAD analizi girdileri
| Santral iç kesiti | mm | 1200×925 |
| Isı değiştirgeci kesiti | mm | 1090×815 |
| Hava debisi | m3/h | 8325 |
| Santral iç hava hızı | m/s | 2,083 |
| Isı değiştirgeci hava hızı | m/s | 2,603 |
| Batarya içi mesh yoğunluğu | 1,25 mm2 de 1 nokta | |
| Santral içi mesh yoğunluğu | 31,25 mm2 de 1 nokta |
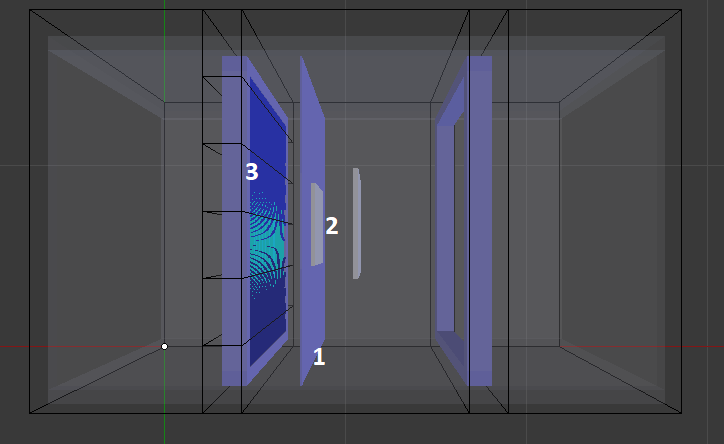
Şekil 6. HAD analizi modellemesi (1- Fan sacı, 2-Fan, 3- Isı Değiştirgeci)
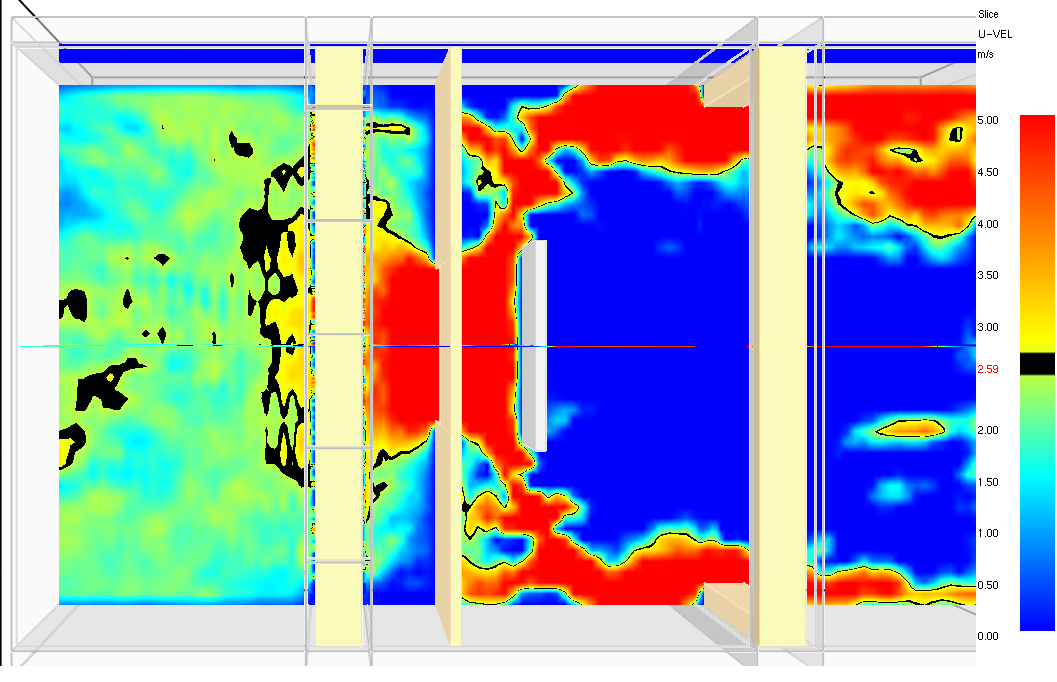
Şekil 7. HAD analizi ile kesit içerisindeki ısı degiştirgecinin üzerinden geçen hava dağılımı görsel
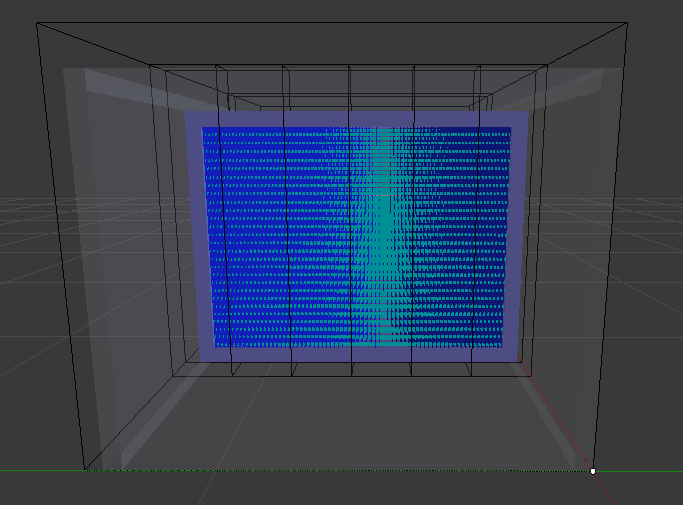
Şekil 8. HAD analizi ısı değiştirgeci ön yüzeyi
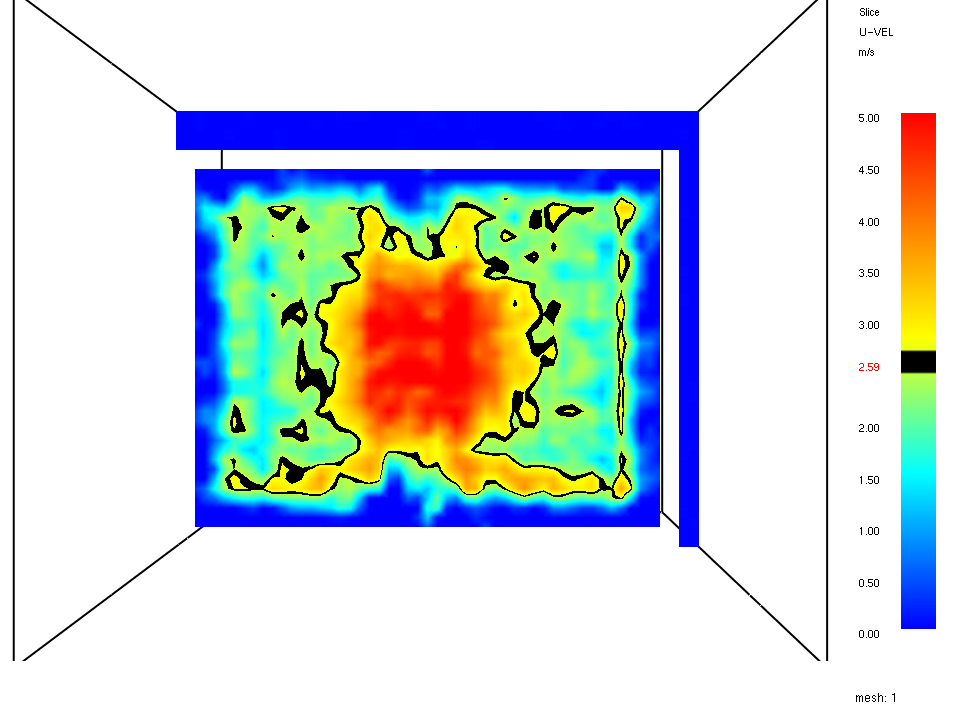
Şekil 9. HAD analizi ile ısı değiştirgeci ön yüzeyindeki hava dağılımı
Tablo 2. Modellenen ısı değiştirgeci notasyonu
| Boru enine mesafe | mm | 25 |
| Boru dikine mesafe | mm | 22 |
| Boru çapı | inç | 3/8 |
| Lamel boyu | mm | 980 |
| Lamel aralığı | mm | 5 |
| Boru sayısı | 32 | |
| Sıra sayısı | 6 |
Buharlaştırıcı ve Yoğuşturucu Simülasyonu
Fan önündeki bir ısı değiştirgeci üzerinden geçen hava akışı simüle edilmiş ve ısı değiştirgecinin üzerindeki hava dağılımının homojen olmadığı belirtilmiştir. Homojen olmayan hava dağılımı ya da farklı pas sayılarına sahip devrelerde akışkan debileri farklılıklar göstermektedir. Bu da soğutucu akışkanın ısı değiştirgecinin her kesidinde ayrı buharlaşma ya da yoğuşma sıcaklığında çalışmasına sebep olmaktadır. Bu çalışma da her devrede soğutucu akışkanın takip ettiği yol, simülasyon programına tanıtılmış, hava dağılımının eşit olduğu ve olmadığı durumlar göz önüne alınarak hesaplamalar yapılmıştır.
Buharlaştırıcı ve Yoğuşturucu Girdileri
Bu çalışmada kullanılan buharlaştırıcı ve yoğuşturucu geometrik özellikleri Tablo 3’te verilmiştir. Şekil 10’da ise hava akış yönleri ile her devreye yönelik boru giriş-çıkış yönleri tarif edilmiştir. Boru iz takibinde ‘Z’ tipi devreleme kullanılmış, soğutucu akışkan olarak R410A seçilmiştir.
Tablo 3. Buharlaştırıcı ve yoğuşturucu geometrik özellikleri
| Açıklama | Kondenser | Evaporator | Br |
| Sıra Sayısı | 4 | 4 | ad |
| Tüp sayısı | 18 | 12 | ad |
| Lamel boyu | 920 | 800 | mm |
| Boru et kalınlığı | 0,4 | 0,35 | mm |
| Boru dış çapı | 9,52 | 9,52 | mm |
| Boru enine mesafe | 22 | 22 | mm |
| Boru yüksekliğine mesafe | 25 | 25 | mm |
| Devre sayısı | 3 | 6 | |
| Lamel kalınlığı | 0,1 | 0,1 | mm |
| Lamel arası | 2,1 | 2,1 | mm |
| Kanatçık tipi | Dalgalı | Dalgalı | |
| Dalga üçgen enine mesafesi | 6,24 | 6,24 | mm |
| Dalga açısı | 9,2 | 9,2 | Derece |
| Dalga yüksekliği | 1 | 1 | mm |
Tablo 4. Buharlaştırıcı ve yoğuşturucu akışkan-hava giriş değerleri
| Yoğuşturucu | Akışkan giriş sıcaklığı | °C | 80 |
| Akışkan giriş faz değişim sıcaklığı | °C | 50 | |
| Akışkan debisi | kg/h | 275 | |
| Hava debisi | m3/h | 4000 | |
| Hava giriş koşulları | °C/%RH | 35/40 | |
| Buharlaştırıcı | Akışkan giriş buhar oranı | % | 0,29 |
| Akışkan giriş faz değişim sıcaklığı | °C | 6 | |
| Akışkan debisi | kg/h | 275 | |
| Hava debisi | m3/h | 2000 | |
| Hava giriş koşulları | °C/%RH | 27/50 |
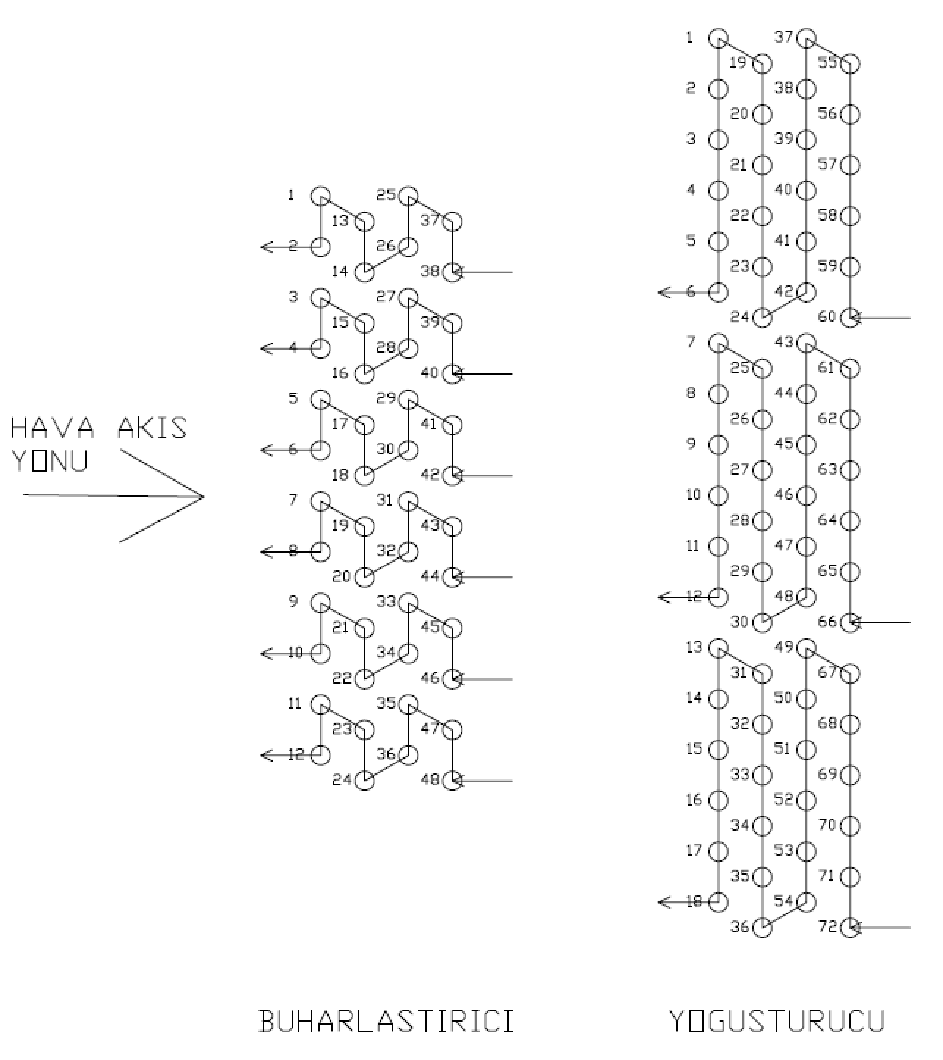
Şekil 10. Simülasyonda kullanılan ısı değiştirgeçlerinin devrelemesi
Buharlaştırıcı ve Yoğuşturucu Hava Dağılımının Kapasiteye Etkisi
Homojen hava dağılımının gerçekleştiği ısı değiştirgeçlerinde soğutucu akışkan, her devrede birebir aynı fiziksel değişimi sağlamaktadır. Homojen olmayan hava akışında ise, soğutucu akışkan, ısı değiştirgeçlerinin her devresinde farklı fiziksel özelliklerle devrelerden çıkmaktadır. Tablo 5’te ısı değiştirgeçlerine giren hava debilerinin oranları havanın ilk girdiği borulara göre HAD anailizinden de çıkan sonuçlar baz alınarak yaklaşık olarak verilmiştir. Devre ve boru adetleri sebebiyle hesaplama sonuç raporu uzun çıktılara sahip olacağından, HAD analizinde gerçek bir örnek simüle edilirken, simülasyon programında, daha küçük geometrilere sahip ısı değiştirgeçleri kullanılmış ve hava akışına referans olması amacıyla HAD analizi sonuçları kullanılmıştır. Hava dağılımı yaklaşık değerleri atanırken ilk borulara değer atanmış ve arkasındaki boruların, ilk sıradaki borulardaki hava dağılım oranlarına benzer olacağı kabul edilmiştir.
Tablo 5. Buharlaştırıcı ve yoğuşturucudaki borulara hava giriş oranları
| Boru numarası | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Yoğuşturucu hava debisi oranı | 0,7 | 0,7 | 0,7 | 0,9 | 0,9 | 0,9 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1 | 1 | 1 | 0,8 | 0,8 | 0,8 |
| Buharlaştırıcı hava debisi oranı | 0,8 | 0,8 | 0,9 | 0,9 | 1,3 | 1,3 | 1,5 | 1,5 | 0,8 | 0,8 | 0,7 | 0,7 |
Tablo 6. Homojen ve homojen olmayan hava dağılımı etkisindeki yoğuşturucudan,iş akışkanı çıkış koşulları ve kapasite
| Yoğuşturucu | ||||||
| Hava dağılımı | Devre no | Kapasite | Çıkış buhar oranı | Çıkış yoğuşma sıcaklığı | Aşırı soğutma sıcaklığı | Kütlesel debi |
| kW | % | °C | °C | kg/h | ||
| Homojen olmayan | 1.devre | 4,44 | 0,030962 | 49,3 | 0 | 88,01 |
| 2.devre | 5,56 | 0 | 49,3 | 9,8 | 97,35 | |
| 3.devre | 4,75 | 0 | 49,3 | 2,4 | 89,63 | |
| Kollektör çıkışı | 14,75 | 0 | 49,3 | 3,52 | 275 | |
| Homojen | 15,03 | 1 | 49,3 | 5,3 | 275 | |
| Fark | 1,90% | 50,57% | ||||
Tablo 7. Homojen ve homojen olmayan hava dağılımı etkisindeki buharlaştırıcıdan, akışkan çıkış koşulları ve kapasite
| Buharlaştırıcı | ||||||
| Hava dağılımı | Devre no | Kapasite | Çıkış buhar oranı | Çıkış buharlaşma sıcaklığı | Aşırı kızdırma sıcaklığı | Kütlesel debi |
| kW | % | °C | °C | kg/h | ||
| Homojen olmayan | 1 | 2,33 | 0,981267 | 5,55 | 0 | 58,4 |
| 2 | 2,47 | 1 | 5,55 | 4,55 | 58,33 | |
| 3 | 2,61 | 1 | 5,55 | 13,31 | 57,81 | |
| 4 | 2,63 | 1 | 5,55 | 13,66 | 58,17 | |
| 5 | 2,33 | 0,981267 | 5,55 | 0 | 58,4 | |
| 6 | 2,24 | 0,950337 | 5,54 | 0 | 58,88 | |
| Kollektör çıkışı | 14,61 | 1 | 5,55 | 2,2 | 350 | |
| Homojen | 14,82 | 1 | 5,55 | 10,52 | 350 | |
| Fark | 1,44% | 378,18% | ||||
Tablo 6 ve 7’de görüldüğü üzere yoğuşturucu ve buharlaştırıcıda hava akışınının homojen ya da homojen olmaması durumlarına göre soğutucu akışkanın çıkış koşulları değişmektedir. Homojen hava dağılımlı yoğuşturucu da aşırı soğutma miktarı 5,3°C iken, homojen olmayan hava dağılımında bu değer 3,52°C’dır. Buharlaştırıcı da ise homojen hava dağılımında aşırı kızdırma miktarı 10,52°C iken, homojen olmayan hava dağılımında bu değer 2,2°C olmaktadır.
Sonuçlar
Bu çalışmada, endüstriyel ve ev tipi ısı pompası cihazlarında en çok kullanılan kanatçıklı borulu ısı değiştirgeçlerinin piyasada kullanılan seçim programlarından farklı olarak, simülasyonu yapılmıştır. Buharlaştırıcı ve yoğuşturucu olarak iki ısı değiştirgecinde akışkan durumu simüle edilmiş, homojen ve homojen olmayan hava dağılımlarına göre akışkanın fiziksel özellikleri irdelenmiştir. Homojen olmayan hava dağılımına sahip ısı değiştirgecinin kapasitesi, homojen olan duruma göre %2 metrebesinde farklılık göstermiştir. Bu fark, havanın homojen olmayan dağılımdaki değerlerin düzensizlik formuna göre artış gösterecektir. Hava akışının homojene yakın olduğu durumda ise sistem performansı artacak ve verimlilik değerleri üzerinde artış gözlenecektir.
Kaynaklar
ARI. 2001. Forced-circulation air-cooling and air-heating coils, ARI standard 410. Virginia : Air-conditioning and refrigeration institute, 2001.
Condensation in horizontal tubes, part 2: new heat transfer model based on flow regimes. Thome, J.R., Hajal, J.E. ve Cavallini, A. 2003. 2003, International journal of heat and mass transfer, s. 3365-3387.
Domanski, P. A. ve Didion, D. 1983. Computer Modeling of the Vapor compression cycle with constant flow are expansion device. 1983, Cilt 155.
Domanski, P. A.; Yashar, D. 2004. An optimized design of finned tube evaporators using the learnable evolution model. 2004, s. 201-211.
Emerson. [Çevrimiçi] https://climate.emerson.com/documents/zp-r410a-scroll-compressors-range-en-gb-4763438.pdf.
Finite circular fin method for wavy fin-and-tube heat exchangers under fully and partially wet surface conditions. Pirompugd, W., Wang, C. C. ve Wongwises, S. 2008. 2008, International Journal of Heat and Mass Transfer, s. 4002-4017.
Fischer, S.K., Rice, C.K. ve Jackson, W.L. 1988. The Oak ridge heatpump design model: Mark III version program documentation. basım yeri bilinmiyor : Oak Ridge Natioanal Laborotory, 1988.
Frascold. [Çevrimiçi] https://www.frascold.it/public/files/files/FCAT250_02_EN.pdf.
Gnielinski, V. 1976. New equation for heat and mass transfer in turbulent pipe and channel flow. 1976, pp. 359-368.
Harms, T. M., Groll, E. A. ve Braun, J.E. 2003. Accurate charge inventory modeling for unitary air conditioners. 2003.
Incorpera, Frank P., ve diğerleri. 2006. Heat Exchangers. Fundementals of heat and mass transfer. basım yeri bilinmiyor : Daniel Sayre, 2006, s. 686-706.
Jiang, H., Vikrant, A. ve Radermacher, R. 2006. CoilDesigner: a general-purpose simulation and design tool for air-to-refrigerant heat exchangers. 2006.
Kakac, S. 2002. Heat Transfer Enhancement of Heat Exchangers. 2002, s. 141-162.
Liang, S. Y., Wong, T. N. ve Nanyang. 1998. Study of refrigerant circuitry of evaporator coils with a distrubuted simulation model. 1998.
McQuiston, F.C. and Parker. 1994. Heating, Ventilating, and Air-conditioning,4th ed. Chapter 14. 1994, s. 571.
Mullen, C.E., ve diğerleri. 1997. Development and validation of a room air conditioning simulation model. 1997.
Pirompugd, W. ve C.C. Wang, S. Wongwises. 2009. A review on reduction method for heat and mass transfer characteristics of fin and tube heat exchangers under dehumidifying conditions. 2009, s. 2370-2378.
Pirompugd, W. ve Wongwises, S. 2016. Actual dry-bulb temperature and equivalent dry-bulb temperature methods for wavy fin-and-tube heat exchangers with dehumidification. 2016, s. 675-685.
Pirompugd, W., Wang, C.C. ve Wongwises, S. 2015. The new mathematical models for plain fin and tube heat exchangers with dehumidification. 2015, s. 1-11.
Ragazzi, F. ve Pedersen, C.O. 1991. Modular based computer simulation of an air cooled condenser. 1991.
Schmidt, ThE. 1949. Heat transfer calculations for extended surfaces. 1949, s. 351-357.
Shah, R. K. ve Sekulic, D. P. 2003. Fundemantals of heat exchanger design. 2003.
Souza, A. L., ve diğerleri. 1992. Pressure drop during two-phase flow of refrigerants in horizontal smooth tubes. 1992.
Thome, J.R. ve L. Wotjan, T. Ursenbacher. 2005. Investigation of flow boiling in horizontal tubes: Part I A new diabatic two-phase flow pattern map. 2005, s. 2955-2969.
—. 2005. Investigation of flow boiling in horizontal tubes: Part II Development of a new heat transfer model for stratified-wavy, dryout and mist flow regimes. 2005, s. 2970-2985.
Thome, J.R. ve Quiben, J.M. 2007. Flow pattern based two-phase frictional pressure drop model for horizontal tubes, Part II: New phenomenological model. 2007, s. 1060-1072.
—. 2007. Flow pattern based two-phase frictional pressure drop model for horizontal tubes. Part I: Diabatic and adiabatic experimental study. 2007, s. 1049-1059.
Thome, J.R., Hajal, J.E. ve Cavallini, A. 2003. Condensation in horizontal tubes, part 1: two phase flow pattern map. 2003, s. 3349-3363.
—. 2003. Condensation in horizontal tubes, part 2: new heat transfer model based on flow regimes. 2003, s. 3365-3387.
Wang, C. C. 1999. On the airside performance of fin and tube heat exchangers. 1999, s. 141-162.
—. 2000. Recent progress on the air side performance of fin and tube heat exchangers. 2000, s. 57-84.
Wang, C.C. ve Y.M. Hwang, Y. Lin. 2002. Empirical correlations for heat transfer and flow friction characteristics of herringbone wavy fin and tube heat exchangers. 2002, s. 673-680.
Wang, C.C., Hsieh, Y. ve Lin, Y. 1997. Performance of plate finned tube heat exchangers under dehumidifying conditions. 1997, s. 109-117.
Wang, C.C., Lin, Y. ve Lee, C.J. 1999. Heat and momentum transfer for compact louvered fin and tube heat exchangers in wet conditions. 1999, s. 3443-3452.
Wang, C.C., ve diğerleri. 1999. Airside Performance of Herringbone Fin-and-Tube Heat. 1999, s. 1225-1230.
Wang, C.C., ve diğerleri. 2001. Parametric study of the air ide performance of slit fin and tube heat exchangers in wet conditions. 2001, s. 1111-1121.
Zivi, S.M. 1964. Estimation of steady state steam void fraction by means of the principle minimum entropy production. 1964, s. 247-251.
Soykan Yaşar /Makine Yüksek Mühendisi
İstanbul Teknik Üniversitesi Gemi İnş. ve Gemi Mak. Mühendisliği bölümünden 2012 yılında mezun olmuştur. Ardından 2019 yılında IYTE Makine Mühendisliği yüksek lisans programını bitirmiştir. 6 yıl İmbat Soğutma A.Ş’ de ArGe mühendisliği yapmıştır. Temmuz 2019’dan beri ATC A.Ş’ de Proje,Planlama ve Arge bölümlerini koordine etmektedir.
Artur Altunkeser/Makine Mühendisi
1971 İstanbul doğumludur. 1993 yılında Boğaziçi Üniversitesi Makine Mühendisliği Bölümünden lisans derecesini almıştır. 1995 yılında Boğaziçi Üniversitesinde MBA yapmıştır. ATC Air Trade -Centre kurucu ortağıdır. Evli ve bir kız çocuk babasıdır.
Orhan Altunkaynak/Makine Mühendisi
Selçuk Üniversitesi Makine Mühendisliği bölümünden 2016 yılında mezun olmuştur. 21 Mart 2016’dan beri ATC A.Ş’ de Teknik ve Satış Mühendisi olarak Jet Fanlı Otopark Havalandırma sistemleri alanında çalışmaktadır.
Doç. Dr. Erdal ÇETKİN
Doktora derecesini Duke Üniversitesi Makine Mühendisliği ve Malzeme Bilimleri bölümünden 2013 yılında Termo-Akişkan alanından almıştır. 2013 yılından itibaren İzmir Yüksek Teknoloji Enstitüsü Makine Mühendisliği Bölümü’nde öğretim üyesi olarak görev yapmaktadır. Termo-Akişkan alanında otuza yakın uluslararası hakemli dergilerde yayınlanmis makalesi, beş adet patent başvurusu bulunmaktadır. Çeşitli uluslararası dergilerin editör kurullarında görev almaktadır.